How to extract datasheet information then use linear and power equations to adjust ppm of MQ sensors depending on temperature and humidity
I dedicated some of my previous posts to MQ gas sensors. These devices are cheap and can be bought on PCB modules, which implement a simple comparator circuit in order to provide a digital output. However, the usability of these modules is rather limited, knowing that some of the sensors from MQ family require variable heater voltage. More than this, at power-up the resistance of the sensor is low until the heater reaches working temperature, therefore the comparator output of a sensor module will trigger a false alarm.
Although this is not an important limitation, the modules do not take into account the variation of sensor resistance based on environment temperature and humidity. To do this, a microcontroller must sample the sensor resistance through an ADC and estimate gas concentration. This post continues a previous one in which I estimated gas ppm after extracting sensitivity data from datasheet graphs. However...
As I mentioned in my previous posts, there are two manufacturers of these sensors. And their sensitivity measurements are different. Here comes the surprise. Winsen has the same graph of temperature and humidity influence in all datasheets, the same for all sensors. Hanwei, on the other hand, has different graphs and there is a visible difference between the variation trends between manufacturers. Hopefully, by the end of this post I should have implemented ppm estimation based on the datasheets of both manufacturers so I can make a comparison on my MQ-2. I will continue with alcohol ppm estimation, even though this sensor is designed for other substances. I found it to be sensitive enough to isopropyl alcohol.
Using the method described in the previous post, these are the equations for both manufacturers (MQ-2, alcohol):
- Winsen: Rs/Ro = 10.2889924963885 ppm^-0.552464627410705 (Ro here is sensor resistance in clean air, at 20±2°C and 55±5% RH).
- Hanwei: Rs/Ro = 20.9733672651754 ppm^-0.372095603150543 (Ro here is sensor resistance in 1000 ppm H2, at 20°C and 65% RH; sensor resistance in clean air at the same temperature and humidity is 9.58 times higher).
Winsen
Now, it's time to plot dependence on temperature and humidity. I started with Winsen since their temperature graph seems to follow more or less a linear equation.
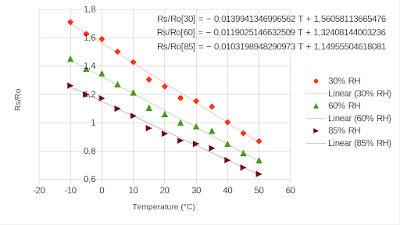 |
| Winsen MQ-2 temperature dependence |
In this graph, the sensor is exposed to 2000 ppm of propane. Rs is its resistance at different temperature and humidity, while Ro is resistance at 20°C and 55% RH. Unfortunately, there is something very wrong here: Rs/Ro is not 1 at specified test conditions... Anyway, that's about temperature. Let's rearrange the data to get and idea of humidity influence.
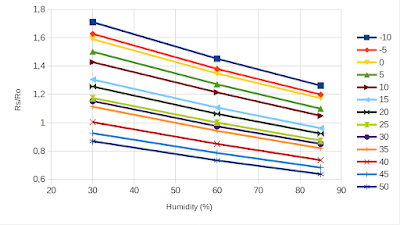 |
| Winsen MQ-2 humidity dependence |
For all temperatures, the humidity dependence looks linear, although only three measuring points are provided (30, 60 and 85% RH). I am not going to compute equations for each, since it is not useful. Instead, I will return to the temperature equations above and plot their coefficients (which should also be linear).
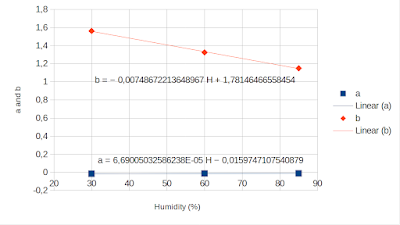 |
| MQ-2 temperature function coefficients |
Using these we can create the equation Rs/Ro = aT+b, where a and b are humidity dependent. The final formula looks as follows:
This translates into code as follows, completing the previously developed sketch:
float correctionFactorTH_Winsen(float temp, float hum) {
const float aaH = 0.0000669005032586238;
const float baH = -0.0159747107540879;
const float abH = -0.00748672213648967;
const float bbH = 1.78146466558454;
return (aaH * hum * temp) + (baH * temp) + (abH * hum) + bbH;
}
int alcoholPPM_Winsen(float Rs_real, float Ro_standard, float temp, float hum) {
const float slope = -0.552464627410705;
const float scale = 10.2889924963885;
Rs_real = Rs_real / correctionFactorTH_Winsen(temp, hum);
return (int)pow(Rs_real / (Ro_standard * scale), (1 / slope));
}
Good or bad, keep in mind that the above correction factor calculation is suitable for all MQ sensors from Winsen.
Hanwei
Fortunately their graphs match the description of test conditions. Unfortunately they didn't bother to make measurement at more than two humidity values. Here is the re-plotted graph for MQ-2 (note that each of their sensors has a different graph).
 |
| Hanwei MQ-2 temperature and humidity variation |
In this graph, the sensor is exposed to 1000 ppm of H2. Rs is its resistance at different temperature and humidity, while Ro is resistance at 20°C and 33% RH. As you can see, in order to be able to get accurate equations, I had to convert temperatures to degrees Fahrenheit (to get rid of negative values). The dependence is clearly not linear for temperature. I can't say the same for humidity. With only two sampled values, I cannot make any assumptions, so I will consider linear dependency.
Using the method described above, I will use humidity to compute scale and slope of temperature function. Without too much details, here is the code:
float correctionFactorTH_Hanwei(float temp, float hum) {
float scale = -0.00699088200923904 * hum + 4.01118163062014;
float slope = 0.00000984021398498172 * hum - 0.303183822378689;
// don't forget to convert temperature to Fahrenheit
return scale * pow((1.8 * temp + 32), slope);
}
int alcoholPPM_Hanwei(float Rs_real, float Ro_standard, float temp, float hum) {
const float slope = -0.372095603150543;
const float scale = 20.9733672651754;
Rs_real = Rs_real / correctionFactorTH_Hanwei(temp, hum);
return (int)pow(Rs_real / (Ro_standard * scale), (1 / slope));
}
I included both of these routines in an Arduino sketch. I added a DHT22 sensor to get temperature and humidity.
Conclusion
Given the amount of computation needed to take into account the influence of temperature and humidity on their resistance, I don't even think this should be implemented in practice with MQ sensors. Especially with 8-bit microcontrollers. Important variation of environmental temperature and humidity is needed to determine a significant change in sensor resistance. And, as I probably said before, tin dioxide sensors are neither gas specific, neither precise enough to give an accurate reading even after all possible corrections are applied.
To make things even more harder, datasheets do not contain sufficient information to allow making accurate ppm estimations. Nevertheless, this was a fun way to learn about these sensors. I'm just kidding... it can't be fun with all that math. And by the way, I don't even know whether I got it right.
Finally, the code is here.



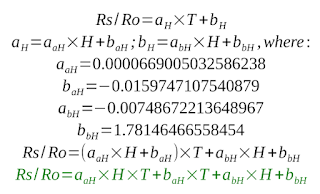



hello, I dont really understand how you get the equation for linear (a), and the following numbers from the hanwei function: float scale = -0.00699088200923904 * hum + 4.01118163062014;
ReplyDeletefloat slope = 0.00000984021398498172 * hum - 0.303183822378689;
I agree. I don't get it either.
Deletewhat i did is calculate the Ro/Rs for given temperature at both humidity 33% and 85%. Then linearly interpolate between the both( Rs/Ro(33%) and Rs/Ro(85%) ) for given humidity( for example 65%).
I haven't tested with calibration gas.